Dalam analisis data statistik, terdapat banyak sekali metode dan penggunaan model statistik. Karena begitu banyaknya model analisis, para mahasiswa seringkali merasa bahwa statistik adalah mata kuliah yang sangat sulit dan sukar untuk dipahami. Padahal dalam penggunaan model atau persamaan dalam menganalisis data statistik kita hanya perlu mengetahui apa tujuan dari analisis statistik kita, baru kemudian memilih model yang sesuai dengan tujuan penelitian kita tersebut.
Pada kesempatan ini, penulis akan membahas mengenai model autoregresif dan distributed-lag. Kedua model tersebut adalah model analisis statistik yang digunakan untuk menunjukan hubungan atau pengaruh kondisi saat ini dan kondisi di masa lampau terhadap kondisi saat ini. Sebagai contoh, ketika kita akan menganalisis pertumbuhan ekonomi tahun 2017 yang dipengaruhi oleh pertumbuhan ekonomi tahun 2016 atau dipengaruhi oleh jumlah investasi tahun 2017 dan jumlah investasi tahun 2016.
sedangkan perbedaan dari kedua model tersebut adalah jika model regresinya menggunakan bukan hanya data saat ini melainkan juga jada sebelumnya dari variabel independen atau biasa juga disebut explanatory disebut sebagai model distributed-lag (lag terdistribusi). sedangkan jika suatu model regresi dengan data time series menggunakan satu atau lebih lag (nilai masa lampau) dari vaiabel dependen diantara variabel independen disebut sebagai model autoregresif.
Berikut adalah contoh dari kedua model tersebut:
Model Distributed-lag Yt = α + β0Xt + β1Xt−1 + β2Xt−2 + ut
Model Autoregresif Yt = α + βXt + γYt−1 + ut
Pada model distributed lag, Xt adalah nilai dari X saat ini sedangkan Xt-1alah nilai dari X sebelumnya. Berbeda dengan model autoregresif, variabel yang digunakan untuk menjelaskan Y bukanhanya variabel X yang berkedudukan sebagai variabel independen tetapi juga nilai dari Y itu sendiri pada waktu sebelumnya yang dinotasikan sebagai Yt-1.
koefisien α disebut juga dengan konstanta yang menunjukan bahwa meskipun tidak ada perubahan variabel independen maka variabel dependennya tetap akan berubah sebesar α sementara Ut adalah variabel lain yang tidak dimasukkan kedalam model. Lebih lanjut, dalam kedua model tersebut dikenal juga efek jangka pendek dan efek jangka panjang yang dinotasikan dengan β. Efek jangka pendek disebut juga dengan impact atau multiplier yang dinotasikan dengan β0. Sedangkan efek jangka panjangnya adalah jumlah dari keluruhan nilai secara matematis adalah sebagai berikut:
Untuk mempermudah pemahaman kita menganai kedua model tersebut, berikut adalah contoh analisis menggunakan model autoregresif dan distributed lag. Misalkan kita memiliki data konsumsi dan data pendapatan masyarakat dari tahun 1954 hingga 1994 yang masing-masing memiliki simbol CONS untuk konsumsi dan INCO untuk pendapatan. Dengan asumsi CONS=f(INCO), dibaca CONS adalah fungsi dari INCO.
Contoh model distributed lag (dengan alat bantu eviews)
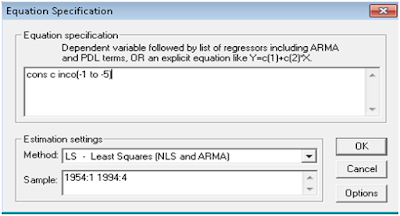
Setelah melakukan input data, klik Quick kedmudian pilih Estimate Equation maka akan muncul menu seperti ini :
Kemudian tuliskan model yang akan kita gunakan. Dalam model distributed-lag, kita dapat menuliskan pada eviews dengan persamaan:
cons c inco(-1 to -5)
Kemudian klik ok, maka akan muncul hasil seperti ini:
|
Dependent Variable: CONS
|
||||
|
Method: Least Squares
|
||||
|
Date: 04/15/17 Time: 10:04
|
||||
|
Sample(adjusted): 1955:2 1994:4
|
||||
|
Included observations: 153
|
||||
|
Excluded observations: 6 after adjusting endpoints
|
||||
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
94.64449
|
45.46218
|
2.081829
|
0.0391
|
|
INCO(-1)
|
-0.467142
|
0.296406
|
-1.576021
|
0.1172
|
|
INCO(-2)
|
0.312630
|
0.297059
|
1.052418
|
0.2943
|
|
INCO(-3)
|
0.182574
|
0.296820
|
0.615101
|
0.5394
|
|
INCO(-4)
|
0.210248
|
0.297609
|
0.706456
|
0.4810
|
|
INCO(-5)
|
-0.475392
|
0.297477
|
-1.598078
|
0.1122
|
|
R-squared
|
0.046755
|
Mean dependent var
|
78.35744
|
|
|
Adjusted R-squared
|
0.014332
|
S.D. dependent var
|
83.42334
|
|
|
S.E. of regression
|
82.82339
|
Akaike info criterion
|
11.70972
|
|
|
Sum squared resid
|
1008378.
|
Schwarz criterion
|
11.82856
|
|
|
Log likelihood
|
-889.7939
|
F-statistic
|
1.442018
|
|
|
Durbin-Watson stat
|
1.958966
|
Prob(F-statistic)
|
0.212580
|
|
Maka hasil estimasi model distributed lag nya adalah sebagai berikut:
cons = 94.644 – 0.467inco+ 0.312inco + 0.182inco + 0.210inco – 0.475inco
Contoh model Autoregresif (dengan alat bantu eviews)
Sama seperti proses dengan model distributed lag, hanya saja yang membedakan adalah model persamaan yang akan kita tuliskan pada eviews.
Dalam model autoregresif, model persamaan yang kita tuliskan adalah
cons c inco cons(-1)
Maka hasilnya akan seperti ini:
|
Dependent Variable: CONS
|
||||
|
Method: Least Squares
|
||||
|
Date: 04/15/17 Time: 10:12
|
||||
|
Sample(adjusted): 1954:2 1994:4
|
||||
|
Included observations: 161
|
||||
|
Excluded observations: 2 after adjusting endpoints
|
||||
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
75.34365
|
24.59443
|
3.063444
|
0.0026
|
|
INCO
|
0.098031
|
0.330623
|
0.296505
|
0.7672
|
|
CONS(-1)
|
-0.001053
|
0.079914
|
-0.013176
|
0.9895
|
|
R-squared
|
0.000556
|
Mean dependent var
|
82.00506
|
|
|
Adjusted R-squared
|
-0.012095
|
S.D. dependent var
|
94.54290
|
|
|
S.E. of regression
|
95.11294
|
Akaike info criterion
|
11.96646
|
|
|
Sum squared resid
|
1429342.
|
Schwarz criterion
|
12.02388
|
|
|
Log likelihood
|
-960.3004
|
F-statistic
|
0.043958
|
|
|
Durbin-Watson stat
|
1.999712
|
Prob(F-statistic)
|
0.957006
|
|
Maka hasil estimasinya adlaah sebagai berikut:
Cons = 75.353 + 0.098inco – 0.00105cons
Demikian penjelasan dan praktik penggunaan model autoregresif dan distributed-lag dan selamat mencoba.
Model Autoregresif dan Distributed-Lag
Model Autoregresif dan Distributed-Lag
Oleh: Guntur Siswanto
Mahasiswa Magister Ekonomi Pembangunan FEB Unila